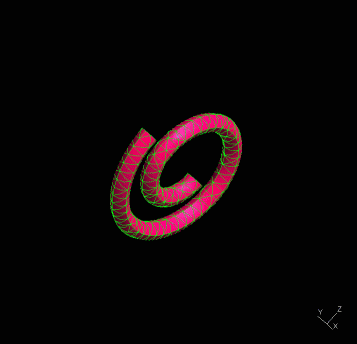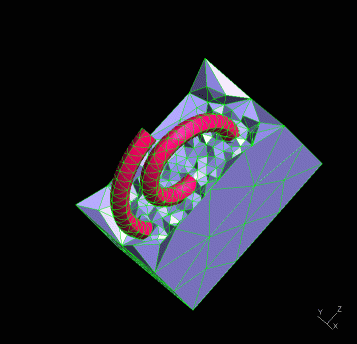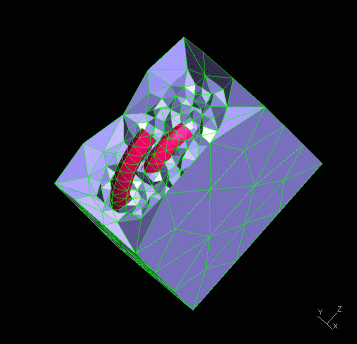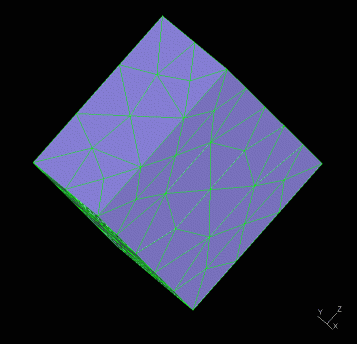From Landau [
1], the finite element method (FEM) is explained as solving a PDE where the whole region or domain is
subsectioned into
smaller areas known as
elements. Next an initial solution is formulated for the PDE in each of the elements. The next step comes in the form of modifying the parameters of the initial formalization known as a
best fit.
Pepper and Heinrich [
2] open their FEM book by explaining that the method is a numerical formulation that solves physics and engineering models described by differential equations (DEs). Similar to finite difference methods (FDM), FEM models a geometric region which is then broken up into a number of
smaller subregions which results in a
network known as a
mesh. One difference between FDM and FEM includes mesh type (geometrically). The FDM requires that the network be made of orthogonal rows and columns (
squares and
rectangles) while the FEM does not require this limitation and can be, in fact, any shape such as
triangles and/or
quadrilaterals in
two dimensions and
tetrahedrons and/or
hexahedrons in
three dimensions. Next, each FE is initialized with an approximate functions of the unknown variables for which to be solved. Expansions determine the variables approximations and appear as a linear or higher-order polynomials functions. These expansions, in turn, depend upon the geometric shape of the elements and location known as nodes. A second difference between FDM and FEM noted by Pepper and Heinrich [
3] entails the solution method. The FEM integrates over each subregion then adds or connects them to make up the whole. This integration and summation engenders a set of finite linear equations per section which can then be solved utilizing linear algebra methods. Jiang [
6] also discusses that FEM does not...
The network of elements and nodes or where these elements connect make up discrete systems such as a trusses, circuits, and fluid transport pipes [
5]. In order to solve for the system variables such as displacements, electric potentials, and pressures, one can begin with a known and simple parameter such as
Hooke’s Law:
\begin{equation} F = \dfrac{\Delta L}{R} = E A \dfrac{\Delta L}{L} \end{equation}
\begin{equation} i = \dfrac{\Delta V}{R} = \dfrac{A}{\rho} \dfrac{\Delta V}{L} \end{equation}
Poiseuille’s Law:
\begin{equation} \dot{m} = \dfrac{\Delta p}{R} = \dfrac{\rho \pi D^4}{128 \mu} \dfrac{\Delta p}{L} \end{equation}
Jiang [
6] notes that FEM has been utilized as one of the most general numerical techniques to solve DEs and done so with great success. Jiang even quotes Oden as
“Perhaps no other family of approximation methods has had a greater impact on the theory and application of numerical methods during the twentieth century”
In progress...to be continued.
References:
[
1] O. C. Zienkiewicz, R. L. Taylor, and J. Z. Zhu.
The Finite Element Method - It’s Basis and Fundamentals, 6th ed. Elsevier Butterworth-Heinemann, Burlington, MA. 2005
[
1] R. H. Landau, M. J. Páez, and C. C. Bordeianu.
A Survey of Computational Physics - Introductory Computational Science, Princeton University Press, Princeton, New Jersey. 2008
[
2] D. W. Pepper and J. C. Heinrich.
The Finite Element Method: Basic Concepts and Applications, Taylor & Francis Hemisphere Publishing Corporation,. 1992
[
4] J. C. Heinrich and D. W. Pepper.
The Intermediate Finite Element Method: Fluid Flow and Heat Transfer Applications, Taylor & Francis Hemisphere Publishing Corporation, Washington, DC. 1999
[
5] G. Comini, S. D. Giudice and C. Nonino.
Finite Element Analysis in Heat Transfer: Basic Formulation & Linear Problems, Taylor & Francis Hemisphere Publishing Corporation, Washington, DC. 1994
[
6] B.-N. Jiang.
The Least-Squares Finite Element Method: Theory and Applications in Computational Fluid Dynamics and Electromagnetics, Springer-Verlag, Berlin, Germany. 1998
[
7] O. C. Zienkiewicz, R. L. Taylor, and P. Nithiarasu.
The Finite Element Method for Fluid Dynamics, (Volume 3) 6th ed. Elsevier Butterworth-Heinemann, Burlington, MA. 2005