Numerical python functions written for compatability with MATLAB commands with the same names.
A blog to record helpful tips/hints/tricks/etc. that I come across during my scientific career regarding science, computers, and research. I love learning and disseminating Knowledge.
Showing posts with label Numerical software. Show all posts
Showing posts with label Numerical software. Show all posts
Thursday, February 2, 2012
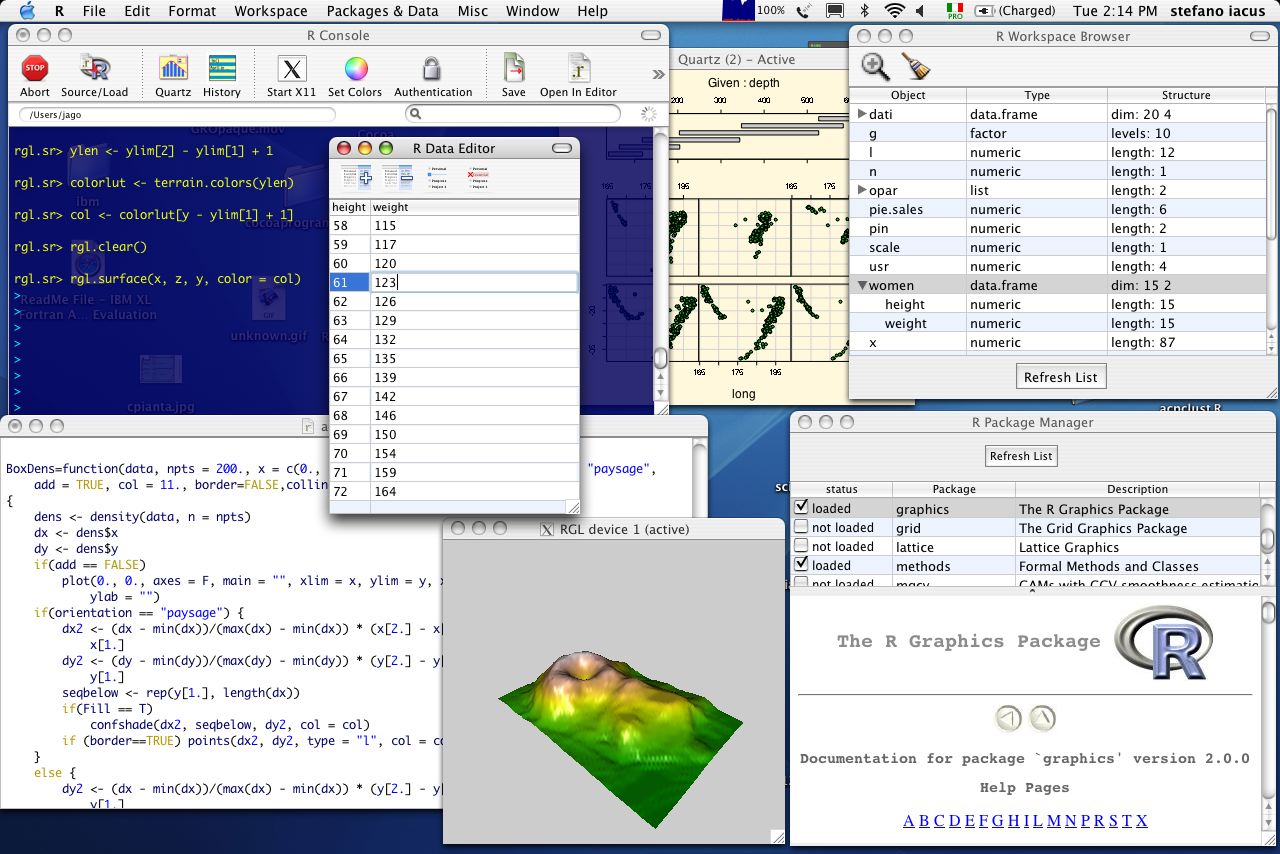
mlab — matplotlib.mlab
mlab — Matplotlib v1.1.0 documentation
Labels:
Math,
Math Software,
MATLAB,
matlibplot,
Numerical software,
Python,
Sage
Tuesday, January 31, 2012
matplotlib: python plotting
http://matplotlib.sourceforge.net/
matplotlib is a python 2D plotting library which produces publication quality figures in a variety of hardcopy formats and interactive environments across platforms. matplotlib can be used in python scripts, the python and ipython shell (ala MATLAB®* or Mathematica®†), web application servers, and six graphical user interface toolkits. matplotlib tries to make easy things easy and hard things possible. You can generate plots, histograms, power spectra, bar charts, errorcharts, scatterplots, etc, with just a few lines of code. For a sampling, see the screenshots, thumbnail gallery, and examples directory
Labels:
matlibplot,
Numerical math,
Numerical software,
plotting,
Programming,
Python
Monday, January 30, 2012
Sage - Declaring a value
So first things first. I simply want to declare a value for something. In this case I want alpha to equal some number.
Hit evaluate and it gives: (1/6)*pi It works!
alpha = 30*pi/180 show(alpha)
Hit evaluate and it gives: (1/6)*pi It works!
Labels:
Math,
Math Software,
Numerical software,
Sage
Sunday, January 15, 2012
SciPy and NumPy - Scientific Tools for Python
Scientific Tools for Python
SciPy (pronounced "Sigh Pie") is open-source software for mathematics, science, and engineering. It is also the name of a very popular conference on scientific programming with Python. The SciPy library depends on NumPy, which provides convenient and fast N-dimensional array manipulation. The SciPy library is built to work with NumPy arrays, and provides many user-friendly and efficient numerical routines such as routines for numerical integration and optimization. Together, they run on all popular operating systems, are quick to install, and are free of charge. NumPy and SciPy are easy to use, but powerful enough to be depended upon by some of the world's leading scientists and engineers. If you need to manipulate numbers on a computer and display or publish the results, give SciPy a try!
Python and Scientific Computing
NumPy and SciPy are two of many open-source packages for scientific computing that use the Python programming language. This website, together with other subdomains of the scipy.org domain, serves as a portal for all scientific computing with Python, not just NumPy and SciPy. The index under Topical Software in the navigation bar lists these domains and other destinations for scientific software using Python.
Good places to start to learn more about SciPy:
- Index of Python packages for scientific computing
- Projects using NumPy / SciPy
- Download NumPy / SciPy
This is a community effort. We seek volunteers at all levels of ability to work on the project, from coding and packaging to documentation, tutorials, recipes, and the web site. Visit the Developer Zone if you are interested in helping out. SciPy is sponsored by Enthought, Inc.SciPy optimization on Ubuntu Linux
NumPy is the fundamental package needed for scientific computing with Python. It contains among other things:
- a powerful N-dimensional array object
- sophisticated (broadcasting) functions
- tools for integrating C/C++ and Fortran code
- useful linear algebra, Fourier transform, and random number capabilities.
Besides its obvious scientific uses, NumPy can also be used as an efficient multi-dimensional container of generic data. Arbitrary data-types can be defined. This allows NumPy to seamlessly and speedily integrate with a wide variety of databases. Numpy is licensed under the BSD license, enabling reuse with few restrictions.
Thursday, December 29, 2011
OpenFOAM and installation of ver. 2.1.0 in Ubuntu 11.10
I've been wanting to install and try this software for awhile now. It is called OpenFOAM and is a free and open source CFD and numerical software. While ANSYS Fluent and others are great and heavily developed, they are quite expensive and un-readily available to many users. I've done some research and OpenFOAM seems to be the leader of the free world. They seem to be very open and constantly updated and developed.
About the OpenFOAM Foundation: http://www.openfoam.org/index.php
About OpenFOAM: http://www.openfoam.com/
The OpenFOAM Team: http://www.openfoam.com/about/
OpenFOAM Services:
I recommend you check this out if you are interested in a free CFD simulator. While it may not have all the bells and whistles of Fluent or other similar software, but I bet you can get just as much done and in the process understand what you are doing much better as it can be the tendency to treat more fancy software as a black box. OpenFOAM has meshing and post processing capabilities (ParaView), supports many imports of meshes from other software, has many solvers, many models, and many libraries, it also has great documentation, tutorials, and community support. Training and customer support is also offered.
To install OpenFOAM simply go to http://www.openfoam.org/download/ where they have choices of the Ubuntu Deb Pack, SuSE RPM Pack, the Source Pack, and the Git Repository. Luckily for us, I am using Ubuntu 11.10 so I simply went to their page for that installation here: http://www.openfoam.org/download/ubuntu.php
I followed the instructions and had no problems until I got to the end where it says Getting Started. It seems to assume that a directory exist in your home directory called OpenFOAM. However, this is not where OpenFOAM was installed as you can see it is installed in /opt/openfoam210 instead. So you need to first create the directory OpenFOAM in your home folder then everything else should be fine in the directions.
This is the link for the documentation (tutorials and more): http://www.openfoam.org/docs/user/
One downside to OpenFOAM is that it is not cross platform. It only works on Linux such as Ubuntu, Fedora, SuSE, etc.
Here is a screen shot showing that OpenFOAM installed into the opt directory.
Here is the message I get after editing the .bashrc file then either typing source $HOME/.bashrc and then typing icoFoam -help or opening a new terminal window then typing icoFoam -help
Screen shot after running blockMesh in the cavity directory.
Viewing the mesh in ParaView by typing paraFoam in the terminal.
After following the instructions on OpenFOAM's user document web page, this is a view of the mesh.
About the OpenFOAM Foundation: http://www.openfoam.org/index.php
The OpenFOAM® Foundation is a non-stock corporation, incorporated on 5th August 2011 in Delaware, USA. It is a nonprofit organization whose “specific objectives and purposes... shall be to promote and manage the free open source distribution of the OpenFOAM software” (Bylaws, Article II). The Foundation has taken on the guardianship of the OpenFOAM software, previously undertaken by OpenCFD Ltd. Through its bylaws, it formalises the commitment, begun by OpenCFD in 2004, to ensure OpenFOAM is free and open source only. It is supported by SGI and lists Mark Barrenechea (CEO, SGI) and Henry Weller (creator of OpenFOAM) amongst its Board of Directors.
The Foundation distributes the current repository version of OpenFOAM (and will distribute future ‘version’ releases of OpenFOAM) under the GNU general public licence (GPL). The GPL gives users the freedom to modify and redistribute the software and a guarantee of continued free use — as long as the terms of the GPL are adhered to. There are two elements to the GPL that provide protection against exploitation by companies including OpenFOAM within non-free and/or closed source software products. First, when any modified version of the software is redistributed, the source code must also be made available by the distributor. Secondly, any modified version can only legally be distributed open source under the GPL and software that links intimately enough to OpenFOAM has to be distributed under the GPL as well.
People and organisations contribute to OpenFOAM on the understanding that their contributions become part of the public commons of free software and are not exploited by producers of non-free software. The Foundation exists to ensure this, adopting a suitably strong, open source license, i.e. the GPL. It will manage the software code base and promote the software, e.g. through its website www.openfoam.org, whose content will grow over time. OpenFOAM Foundation 15th August 2011
About OpenFOAM: http://www.openfoam.com/
The OpenFOAM® (Open Field Operation and Manipulation) CFD Toolbox is a free, open source CFD software package produced by OpenCFD Ltd. It has a large user base across most areas of engineering and science, from both commercial and academic organisations. OpenFOAM has an extensive range of features to solve anything from complex fluid flows involving chemical reactions, turbulence and heat transfer, to solid dynamics and electromagnetics. It includes tools for meshing, notably snappyHexMesh, a parallelised mesher for complex CAD geometries, and for pre- and post-processing. Almost everything (including meshing, and pre- and post-processing) runs in parallel as standard, enabling users to take full advantage of computer hardware at their disposal.
By being open, OpenFOAM offers users complete freedom to customise and extend its existing functionality, either by themselves or through support from OpenCFD. It follows a highly modular code design in which collections of functionality (e.g. numerical methods, meshing, physical models, …) are each compiled into their own shared library. Executable applications are then created that are simply linked to the library functionality. OpenFOAM includes over 80 solver applications that simulate specific problems in engineering mechanics and over 170 utility applications that perform pre- and post-processing tasks, e.g. meshing, data visualisation, etc.
The OpenFOAM Team: http://www.openfoam.com/about/
The OpenFOAM Team produces the OpenFOAM® open source CFD toolbox and distributes it through the OpenFOAM Foundation. The OpenFOAM Team was formed at OpenCFD Ltd, a company established in 2004 to coincide with the release of its OpenFOAM software under general public licence. The company was founded by: Henry Weller, the creator of OpenFOAM and its chief developer from inception to the present day; Chris Greenshields; and, Mattijs Janssens. In 2011, the team moved to SGI Corp, following its acquisition of OpenCFD Ltd.
OpenFOAM Services:
The OpenFOAM Team has unrivalled experience with OpenFOAM. Over the past 7 years they have successfully provided services to numerous science/engineering companies, consultancies and universities. Developments: written over half a million of lines of code. Support: delivered over 10,000 hours of support. Training: delivered over 100 training courses to over 1000 OpenFOAM users. The OpenFOAM Team is Henry Weller, Chris Greenshields, Mattijs Janssens, Andy Heather, Sergio Ferraris, Jenya Collings, Gijs Wierink and Laurence McGlashan.
I recommend you check this out if you are interested in a free CFD simulator. While it may not have all the bells and whistles of Fluent or other similar software, but I bet you can get just as much done and in the process understand what you are doing much better as it can be the tendency to treat more fancy software as a black box. OpenFOAM has meshing and post processing capabilities (ParaView), supports many imports of meshes from other software, has many solvers, many models, and many libraries, it also has great documentation, tutorials, and community support. Training and customer support is also offered.
To install OpenFOAM simply go to http://www.openfoam.org/download/ where they have choices of the Ubuntu Deb Pack, SuSE RPM Pack, the Source Pack, and the Git Repository. Luckily for us, I am using Ubuntu 11.10 so I simply went to their page for that installation here: http://www.openfoam.org/download/ubuntu.php
I followed the instructions and had no problems until I got to the end where it says Getting Started. It seems to assume that a directory exist in your home directory called OpenFOAM. However, this is not where OpenFOAM was installed as you can see it is installed in /opt/openfoam210 instead. So you need to first create the directory OpenFOAM in your home folder then everything else should be fine in the directions.
This is the link for the documentation (tutorials and more): http://www.openfoam.org/docs/user/
One downside to OpenFOAM is that it is not cross platform. It only works on Linux such as Ubuntu, Fedora, SuSE, etc.
Here is a screen shot showing that OpenFOAM installed into the opt directory.
Here is a screen shot showing the /home/timbarber/OpenFoam/timbarber-2.1.0/run/tutorial tree. This is the step where the tutorial material is copied from the /opt/openfoam210 directory.
Screen shot after running blockMesh in the cavity directory.
Viewing the mesh in ParaView by typing paraFoam in the terminal.
After following the instructions on OpenFOAM's user document web page, this is a view of the mesh.
Monday, October 10, 2011
deal.II Homepage
deal.II Homepage: A Finite Element Differential Equations Analysis Library - October 9th, 2011: deal.II 7.1 released
What is deal.II?
deal.II is a C++ program library targeted at the computational solution of partial differential equations using adaptive finite elements. It uses state-of-the-art programming techniques to offer you a modern interface to the complex data structures and algorithms required.
The main aim of deal.II is to enable rapid development of modern finite element codes, using among other aspects adaptive meshes and a wide array of tools classes often used in finite element program. Writing such programs is a non-trivial task, and successful programs tend to become very large and complex. We believe that this is best done using a program library that takes care of the details of grid handling and refinement, handling of degrees of freedom, input of meshes and output of results in graphics formats, and the like. Likewise, support for several space dimensions at once is included in a way such that programs can be written independent of the space dimension without unreasonable penalties on run-time and memory consumption.
deal.II is widely used in many academic and commercial projects. For its creation, its principal authors have received the 2007 J. H. Wilkinson Prize for Numerical Software. It is also part of the industry standard SPEC CPU 2006 benchmark suite used to determine the speed of computers and compilers, and comes pre-installed on the machines offered by the commercial Sun Grid program.
deal.II emerged from work at the Numerical Methods Group at Universität Heidelberg, Germany, which is at the forefront of adaptive finite element methods and error estimators. Today, it is maintained by two of its original authors at Texas A&M University, and dozens of contributors and several hundred users are scattered around the world (see our credits page for a detailed list of people contributing to deal.II).
What deal.II can offer you?
If you are active in the field of adaptive finite element methods, deal.II might be the right library for your projects. Among other features, it offers:
Support for one, two, and three space dimensions, using a unified interface that allows to write programs almost dimension independent.
Handling of locally refined grids, including different adaptive refinement strategies based on local error indicators and error estimators. Both h, p, and hp refinement is fully supported for continuous and discontinuous elements.
Support for a variety of finite elements: Lagrange elements of any order, continuous and discontinuous; Nedelec and Raviart-Thomas elements of any order; elements composed of other elements.
Parallelization on single machine through the Threading Build Blocks and across nodes via MPI. deal.II has been shown to scale to at least 16k processors.
Extensive documentation: all documentation is available online in a logical tree structure to allow fast access to the information you need. If printed it comprises more than 500 pages of tutorials, several reports, and presently some 5,000 pages of programming interface documentation with explanations of all classes, functions, and variables. All documentation comes with the library and is available online locally on your computer after installation.
Modern software techniques that make access to the complex data structures and algorithms as transparent as possible. The use of object oriented programming allows for program structures similar to the structures in mathematical analysis.
A complete stand-alone linear algebra library including sparse matrices, vectors, Krylov subspace solvers, support for blocked systems, and interface to other packages such as Trilinos, PETSc and METIS.
Support for several output formats, including many common formats for visualization of scientific data.
Portable support for a variety of computer platforms and compilers.
Free source code under an Open Source license, and the invitation to contribute to further development of the library.
Saturday, September 24, 2011
Numerical Math - Square wire problem - finite difference method
The square-wire problem is described by the 2-D Laplace and Poisson equations [1].
\begin{equation} \dfrac{\partial^2 U \left( x, y \right)}{\partial x^2} + \dfrac{\partial^2 U \left( x, y \right)}{\partial y^2} = \left\{ \begin{array}{cr} 0 & \text{Laplace's Equation}\\ -4 \pi \rho \left( \mathbf{x} \right) & \text{Poisson's Equation} \end{array} \right. \end{equation}
Next, in order to obtain the second order derivatives a Taylor series expansion with steps of positive and negative values in both \( x \) and \( y \) are executed for \( U \).
\begin{equation} U \left( x + \Delta x, y \right) = U \left( x, y \right) + \dfrac{\partial U}{\partial x} \Delta x + \dfrac{1}{2} \dfrac{\partial^2 U}{\partial x^2} \left( \Delta x \right)^2 + \cdots, \end{equation}
\begin{equation} U \left( x - \Delta x, y \right) = U \left( x, y \right) - \dfrac{\partial U}{\partial x} \Delta x + \dfrac{1}{2} \dfrac{\partial^2 U}{\partial x^2} \left( \Delta x \right)^2 - \cdots, \end{equation}
\begin{equation} U \left( x, y + \Delta y \right) = U \left( x, y \right) + \dfrac{\partial U}{\partial y} \Delta y + \dfrac{1}{2} \dfrac{\partial^2 U}{\partial y^2} \left( \Delta y \right)^2 + \cdots, \end{equation}
\begin{equation} U \left( x, y - \Delta y \right) = U \left( x, y \right) - \dfrac{\partial U}{\partial y} \Delta y + \dfrac{1}{2} \dfrac{\partial^2 U}{\partial y^2} \left( \Delta y \right)^2 - \cdots, \end{equation}
Now, adding both equations each for \( x \) and \( y \) the odd terms cancel, and truncating at \( O \left( \Delta^4 \right) \) obtains
\begin{equation} U \left( x + \Delta x, y \right) + U \left( x - \Delta x, y \right) = 2 U \left( x, y \right) + \dfrac{\partial^2 U}{\partial x^2} \left( \Delta x \right)^2 + O \left( \Delta x^4 \right) \end{equation}
\begin{equation} U \left( x, y + \Delta y \right) + U \left( x, y - \Delta y \right) = 2 U \left( x, y \right) + \dfrac{\partial^2 U}{\partial y^2} \left( \Delta y \right)^2 + O \left( \Delta y^4 \right) \end{equation}
Rearranging to segregate the second derivative engenders
\begin{equation} U \left( x, y + \Delta y \right) + U \left( x, y - \Delta y \right) = 2 U \left( x, y \right) + \dfrac{\partial^2 U}{\partial y^2} \left( \Delta y \right)^2 + O \left( \Delta y^4 \right) \end{equation}
Rearranging to segregate the second derivative engenders
\begin{equation} \dfrac{\partial^2 U}{\partial x^2} \left( \Delta x \right)^2 = U \left( x + \Delta x, y \right) + U \left( x - \Delta x, y \right) - 2 U \left( x, y \right) \end{equation}
\begin{equation} \dfrac{\partial^2 U}{\partial y^2} \left( \Delta y \right)^2 = U \left( x, y + \Delta y \right) + U \left( x, y - \Delta y \right) - 2 U \left( x, y \right) \end{equation}
\begin{equation} \dfrac{\partial^2 U}{\partial y^2} \left( \Delta y \right)^2 = U \left( x, y + \Delta y \right) + U \left( x, y - \Delta y \right) - 2 U \left( x, y \right) \end{equation}
Finally, dividing produces
\begin{equation} \dfrac{\partial^2 U}{\partial x^2} = \dfrac{U \left( x + \Delta x, y \right) + U \left( x - \Delta x, y \right) - 2 U \left( x, y \right)}{\Delta x^2} \end{equation}
\begin{equation} \dfrac{\partial^2 U}{\partial y^2} = \dfrac{U \left( x, y + \Delta y \right) + U \left( x, y - \Delta y \right) - 2 U \left( x, y \right)}{\Delta y^2} \end{equation}
Next, substituting the second order derivatives into the Poisson equation produces
\begin{equation} \begin{array}{l} \dfrac{U \left( x + \Delta x, y \right) + U \left( x - \Delta x, y \right) - 2 U \left( x, y \right)}{\Delta x^2} \\ \hspace{1.15 in} + \dfrac{U \left( x, y + \Delta y \right) + U \left( x, y - \Delta y \right) - 2 U \left( x, y \right)}{\Delta y^2} = -4 \pi \rho \left( x, y \right) \end{array} \end{equation}
If the grid spacing is the same in both the \( x \) and \( y \) coordinates, that is \( \Delta x = \Delta y \), then the equation reduces to
\begin{equation} \begin{array}{l} U \left( x + \Delta, y \right) + U \left( x - \Delta, y \right) + U \left( x, y + \Delta \right) \\ \hspace{2 in} + \hspace{1 mm} U \left( x, y - \Delta \right) - 4 U \left( x, y \right) = -4 \pi \rho \left( x, y \right) \Delta^2 \end{array} \end{equation}
\begin{equation} \begin{array}{l} U \left( x + \Delta, y \right) + U \left( x - \Delta, y \right) + U \left( x, y + \Delta \right) \\ \hspace{2 in} + \hspace{1 mm} U \left( x, y - \Delta \right) - 4 U \left( x, y \right) = -4 \pi \rho \left( x, y \right) \Delta^2 \end{array} \end{equation}
Algebraically, the solution \( U \left( x, y \right) \) can be shown as
\begin{equation} \begin{array}{l} U \left( x, y \right) \simeq \dfrac{1}{4} \left[ U \left( x + \Delta, y \right) + U \left( x - \Delta, y \right) \right. \\ \hspace{2 in} \left. + \hspace{1 mm} U \left( x, y + \Delta \right) + U \left( x, y - \Delta \right) \right] + \pi \rho \left( x, y \right) \Delta^2 \end{array} \end{equation}
Lattice spacings can be identified as \( x = x_0 \pm \Delta \) and \( y = y_0 \pm \Delta \) which correspond to \(i \pm 1 \) and \( j \pm 1 \) where \( i, j = 0, 1, \ldots, N_{max - 1} \). Thus, the finite difference algorithm appears as
\begin{equation} U_{i, j} = \dfrac{1}{4} \left( U_{i + 1, j} + U_{i - 1, j} + U_{i, j + 1} + U_{i, j - 1} \right) + \pi \rho_{i, j}\Delta^2 \end{equation}
However, for simplicity Landau et al just ask to solve for the homogeneous equation
\begin{equation} U_{i, j} = \dfrac{1}{4} \left( U_{i + 1, j} + U_{i - 1, j} + U_{i, j + 1} + U_{i, j - 1} \right) \end{equation}
A few notes here from Landau et al. For one a direct solution cannot be obtain from this algorithm. That is, a process must be repeated several times in order for a solution to converge! Thus, this is where efficiency and proficiency becomes very important in numerical methods.
First, a guess is imposed then swept over the domain which finds values for all variables at each point or node. The solution has "converged" when the current generation does not change compared to the previous generation of values within a "tolerance" or error/precision (absolute value of the difference between old values and new) specified by the user or technique. Another outcome could be that the values emerge as not expected which at that point the user must go back and figure out from where the error is coming. Landau et al give the definition of relaxed as when the first guess has converged into a solution.
Landau et al pose "Does it always converge, and if so, does it converge fast enough to be useful?"
Another important note is the coordinate system used. This problem was done in rectangular Cartesian coordinates. Other problems may work better in other coordinate systems such as cylindrical or spherical depending upon the geometry of the problem in which case the Laplacian expansion \( \Delta^2 \) will be different.
One way to solve the algorithm is to utilize the Jacobi method. This most basic method simply evaluates each point, sweeping across the domain. The initialization and BCs symmetry are preserved in this way. However, in order to speed up this method, a simple modification can be implemented where values that are known from the current run compared to other nodes can be updated immediately. Thus, reducing the amount of needed storage by half since two nodes will be know for one in this case and the previous sweep will not be necessary to store since information is updated instantaneously when available. This technique is called the Gauss-Seidel method. The GS method leads to quicker convergence, less round-off error, and less needed storage. However, symmetry is not conserved which the user hopes does not affected the solution outcome.
If the sweep begins at the top left corner then the GS algorithm looks like
\begin{equation} U_{i, j} = \dfrac{1}{4} \left[ U^{(old)}_{i + 1, j} + U^{(new)}_{i - 1, j} + U^{(old)}_{i, j + 1} + U^{(new)}_{i, j - 1} \right] \end{equation}
\begin{equation} U_{i, j} = \dfrac{1}{4} \left( U_{i + 1, j} + U_{i - 1, j} + U_{i, j + 1} + U_{i, j - 1} \right) + \pi \rho_{i, j}\Delta^2 \end{equation}
However, for simplicity Landau et al just ask to solve for the homogeneous equation
\begin{equation} U_{i, j} = \dfrac{1}{4} \left( U_{i + 1, j} + U_{i - 1, j} + U_{i, j + 1} + U_{i, j - 1} \right) \end{equation}
A few notes here from Landau et al. For one a direct solution cannot be obtain from this algorithm. That is, a process must be repeated several times in order for a solution to converge! Thus, this is where efficiency and proficiency becomes very important in numerical methods.
First, a guess is imposed then swept over the domain which finds values for all variables at each point or node. The solution has "converged" when the current generation does not change compared to the previous generation of values within a "tolerance" or error/precision (absolute value of the difference between old values and new) specified by the user or technique. Another outcome could be that the values emerge as not expected which at that point the user must go back and figure out from where the error is coming. Landau et al give the definition of relaxed as when the first guess has converged into a solution.
Landau et al pose "Does it always converge, and if so, does it converge fast enough to be useful?"
Another important note is the coordinate system used. This problem was done in rectangular Cartesian coordinates. Other problems may work better in other coordinate systems such as cylindrical or spherical depending upon the geometry of the problem in which case the Laplacian expansion \( \Delta^2 \) will be different.
One way to solve the algorithm is to utilize the Jacobi method. This most basic method simply evaluates each point, sweeping across the domain. The initialization and BCs symmetry are preserved in this way. However, in order to speed up this method, a simple modification can be implemented where values that are known from the current run compared to other nodes can be updated immediately. Thus, reducing the amount of needed storage by half since two nodes will be know for one in this case and the previous sweep will not be necessary to store since information is updated instantaneously when available. This technique is called the Gauss-Seidel method. The GS method leads to quicker convergence, less round-off error, and less needed storage. However, symmetry is not conserved which the user hopes does not affected the solution outcome.
If the sweep begins at the top left corner then the GS algorithm looks like
\begin{equation} U_{i, j} = \dfrac{1}{4} \left[ U^{(old)}_{i + 1, j} + U^{(new)}_{i - 1, j} + U^{(old)}_{i, j + 1} + U^{(new)}_{i, j - 1} \right] \end{equation}
Octave code:
%This code was written by Tim Barber for the numerical PDE class taught by Dr. Parigger in the Summer of 2011%This file corresponds specifically to HW set #1
%Problem 1.3 Square Wire Problem: Chapter 17 of the Landau-course bookdiscusses the square-wire problem, viz. elliptic PDE. Section 17.4.2elaborates on the solution using the finite difference method. Your taskhere is to (i) derive the finite difference algorithm Eq. 17.27, (ii)implement the code using source programing (see the listed sourcecode), and (iii) display the results using gnuplot (along the lines ofSection 17.4.2).
clfclcclear%input data manually
N_max = 100;iter = 1000;
%initialize matrix
for i = 1:N_maxfor j = 1:N_maxif j = 100U(i, 100) = 99;elseU(i, j) = 0;j = j + 1;endendi = i +1;end%iterate matrix using the Gauss-Seidel techniquefor n = 1:iter + 1for i = 2:N_max - 1for j = 2:N_max - 1U(i, j) = (1/4)*(U(i + 1, j) + U(i - 1, j)+ U(i, j + 1) + U(i, j - 1));j = j + 1;endi = i +1;endn = n + 1;end%plot of U(x, y)mesh (U)%label title and axestitle('HW 1.3', "fontsize", 20)ylabel('y', "fontsize", 16)xlabel('x', "fontsize", 16)zlabel('U(x, y)', "fontsize", 16)%commands to save plot as a .png fileprint("HW_1_3_mesh.png")replot
References:
[1] R. H. Landau, M. J. Páez, and C. C. Bordeianu. A Survey of Computational Physics -
a Introductory Computational Science, Princeton University Press, Princeton, New Jersey.
2008
Sunday, September 4, 2011
Numerical Mathematics - Solving the heat diffusion equation
This post is influenced by a homework problem from a numerical PDE class I took this past summer (2011). This problem examines the DMOLCH routine and Gear's method for a heat diffusion equation. We are to reproduce data found in a journal paper. The numerics to obtain can be found in the journal article "Temperature distribution in dental tissue after interaction with femtosecond laser pulses" by Pike et al in Applied Optics, Vol. 46, Num. 34, Dec. 2007. I also include some discussion on IMSL, FORTRAN, MOL and many other topics associated with this problem. I will also have individual posts on these topics as well.
IMSL stands for the International Mathematics and Statistics Library and consist of numerous commercial software library utilized in numerical analysis in various programming languages organized by Rogue Wave Software [1, 2]. According to the 2003 Visual Numerics IMSL Fortran Library User’s Guide Math Library Volume 2 of 2 - Mathematical Functions in Fortran [3], the package routine DMOLCH is the double precision version of the routine MOLCH in the Fortran 77 interface which of course is single precision. In the Fortran 90 interface the specific interface names are S MOLCH and D MOLCH for double and single precision, respectively. The routine MOLCH according to the 2003 guide,
The method of lines (MOL) is described by Wouwer et al [5] in the second section of the first chapter in the book entitled Adaptive Method of Lines [6]. The MOL attacks and aims to solve partial differential equations (PDEs) with the form \begin{equation} \textbf{u}_t = \textbf{f}(\textbf{u}), \quad \quad \textbf{x}_l < \textbf{x} < \textbf{x}_r, \quad \quad t > 0 \end{equation} where \begin{align*} \textbf{u}_t &= \dfrac{\partial \textbf{u}}{\partial t} \\ \textbf{u} &= \text{vector of dependent variables} \\ t &= \text{initial value independent variable} \\ \textbf{x}& = \text{boundary value independent variables} \\ \textbf{f} &= \text{spatial differential operator} = \textbf{f} \left( \textbf{x}, t, \textbf{u}, \textbf{u}_x,\textbf{u}_{xx}, \ldots \right) \end{align*} Wouwer et al [5] divide the MOL process into two sections. The first step discretizes the spatial derivatives, \( \textbf{u}_x, \textbf{u}_xx, \ldots \) using finite difference (FD) or finite element (FE) methods. The second step involves integrating the resulting system of semi-discrete ordinary differential equations (ODEs) in the initial value variable wrt to time, \( t \).
As an example of the MOL, Wouwer et al [5] utilize the linear advection equation to demonstrate the process. \[ \dfrac{\partial u}{\partial t} = -v \dfrac{\partial u}{\partial x} \] To begin, the equation is discretized in the spatial realm of \( x \) into an \( N \) number of grid points which are spaced evenly by the distance \( \delta x \). The spatial derivative, \( \partial u/ \partial x \), is then approximated by its second order centered FD beginning at grid point \( i \) up to the maximum discretization point \( N \) so that \[ \dfrac{\partial u}{\partial x} = -v \dfrac{u_{i+1} - u_{i-1}}{2 \Delta x} + O \left( \Delta x^2 \right), \quad i = 1, 2, \cdots, N \] Then assuming a value of \( v = 1 \) and substituting into \( \partial u/\partial t = -v \partial u/\partial x \) results in the equation \[ \dfrac{\mathrm{d} u}{\mathrm{d} t} = -\dfrac{u_{i+1} - u_{i-1}}{2 \Delta x}, \quad i = 1, 2, \cdots, N \]
Wouwer et al [5] next mention that at this point a system of \( N \) ODEs are generated which can then be integrated by an already developed by a library ODE integrator. An initial condition must then be specified next at the \( N \) grid points and the false points \( u_0 \) and \( u_{N + 1} \) for \( i = 1 \) and \( i = N \). Thus, if an example of the equation is solved for two step functions separated by a time interval of \( t = 50 \) or simply a square pulse, with a spatial length of \( N =101 \) or 100 intervals with a length of \( \Delta x \), the solution exhibits oscillatory behavior as seen in the figure by Wouwer et al [5]. This oscillation is of course false and is caused by the numerics of the problem known as a numerical distortion.
1. An ODE is stiff if the step size required for stability is much smaller than the step size required for accuracy.
2. An ODE is stiff if it contains some components of the solution that decay rapidly compared to other components of the solution.
3. A system of ODEs is stiff if at least one eigenvalue of the system is negative and large compared to the other eigen values of the system.
4. From a practical point of view, an ODE is stiff if the step sixe based on cost (i.e., computational time) is too large to obtain an accurate (i.e., stable) solution.
Hoffman [7] also gives a couple of examples.
Also, since it is mentioned let’s talk about Adams methods. According to Iserles [14],
In progress...to be continued.
References:
[1] IMSL Numerical Libraries. 07-23-2011, http://en.wikipedia.org/wiki/IMSL Numerical Libraries
[2] IMSL R Numerical Libraries. imsl-numerical-libraries.aspx 07-23-2011, http://www.roguewave.com/products/
[3] Visual Numerics IMSL Fortran Library User’s Guide Math Library Volume 2 of 2 - Mathematical Functions in Fortran. 07-23-2011, http://www.absoft.com/Support/Documentation/MathV2.pdf, 2003
[4] Visual Numerics IMSL Fortran Numerical Library User’s Guide Math Library Version 7.0. 07-23-2011, http://www.roguewave.com/portals/0/products/imsl-numerical-libraries/fortran-library/docs/7.0/math/math.pdf, 2010
[5] A. Vande Wouwer, P. Saucez, & W. E. Schiesser. Chapter 1 Introduction. A. Vande Wouwer, P. Saucez, & W. E. Schiesser (editors). Adaptive Method of Lines. Chapman & Hall/CRC, Boca Raton, FL. 2001
[6] A. Vande Wouwer, P. Saucez, & W. E. Schiesser (editors). Adaptive Method of Lines. Chapman & Hall/CRC, Boca Raton, FL. 2001
[7] J. D. Hoffman. Numerical Methods for Engineers and Scientists. 2 edition. Marcel Dekker, Inc., New York, NY. 2001
[8] P. Pike, C. Parigger, R. Splinter, and P. Lockhart. Temperature distribution in dental tissue after interaction with femtosecond laser pulses. Applied Optics, Volume 46, Number 34, December 2007
[9] C. W. Gear. Numerical Initial Value Problems in Ordinary Differential Equations, Prentice-Hall, Englewood Cliffs, New Jersey. 1971
[10] K. Velten. Mathematical Modeling and Simulation: Introduction for Scientists and Engineers, Wiley-VCH, Weinheim, Germany. 2009
[11] A. C. Hindmarsh. ODEPACK, a systematized collection of ODE solvers, Scientific Computing, North-Holland, Amsterdam, The Netherlands, pp. 55–64. 1983
[12] L. R. Petzold. Automatic selection of methods for solving stiff and nonstiff systems of ordinary differential equations. SIAM Journal on Scientific and Statistical Computing, 4, 136–48. 1983
[13] K. Soetaert, T. Petzoldt, and R. W. Setzer. Solving Differential Equations in R: Package deSolve. Journal of Statistical Software, 33, 4, February 2010
[14] A. Iserles. A First Course in the Numerical Analysis of Differential Equations. (2nd ed.).
Cambridge University Press, Cambridge, UK. 2009
Additional keywords:
finite difference equations (FDEs), Gear's method, LSODE, LSODA, Adams method, deSolve, R, Maxima, backward differentiation formulas (BDF) method, International Mathematics and Statistics Library (IMSL), Rogue Wave Software, DMOLCH, MOLCH, Fortran, Fortran 90, MMOLCH, Fortran 77, S MOLCH, D MOLCH, S MMOLCH, D MMOLCH, Method of Lines (MOL), Partial Differential Equations (PDEs), Finite Difference (FD), Finite Element (FE), ordinary differential equations (ODEs)
IMSL stands for the International Mathematics and Statistics Library and consist of numerous commercial software library utilized in numerical analysis in various programming languages organized by Rogue Wave Software [1, 2]. According to the 2003 Visual Numerics IMSL Fortran Library User’s Guide Math Library Volume 2 of 2 - Mathematical Functions in Fortran [3], the package routine DMOLCH is the double precision version of the routine MOLCH in the Fortran 77 interface which of course is single precision. In the Fortran 90 interface the specific interface names are S MOLCH and D MOLCH for double and single precision, respectively. The routine MOLCH according to the 2003 guide,
“Solves a system of partial differential equations of the form \( u_t = f \left( x, t, u, u_x, u_{xx} \right) \) using the method of lines. The solution is represented with cubic Hermite polynomials.”According to the 2010 guide, Visual Numerics IMSL Fortran Numerical Library User’s Guide Math Library Version 7.0 [4], the MOLCH routine has been “deprecated” by the new routine MMOLCH, where the definition remains the same as the quote above and the specific F90 interface names for single and double precision are S MMOLCH and D MMOLCH, respectivley.
The method of lines (MOL) is described by Wouwer et al [5] in the second section of the first chapter in the book entitled Adaptive Method of Lines [6]. The MOL attacks and aims to solve partial differential equations (PDEs) with the form \begin{equation} \textbf{u}_t = \textbf{f}(\textbf{u}), \quad \quad \textbf{x}_l < \textbf{x} < \textbf{x}_r, \quad \quad t > 0 \end{equation} where \begin{align*} \textbf{u}_t &= \dfrac{\partial \textbf{u}}{\partial t} \\ \textbf{u} &= \text{vector of dependent variables} \\ t &= \text{initial value independent variable} \\ \textbf{x}& = \text{boundary value independent variables} \\ \textbf{f} &= \text{spatial differential operator} = \textbf{f} \left( \textbf{x}, t, \textbf{u}, \textbf{u}_x,\textbf{u}_{xx}, \ldots \right) \end{align*} Wouwer et al [5] divide the MOL process into two sections. The first step discretizes the spatial derivatives, \( \textbf{u}_x, \textbf{u}_xx, \ldots \) using finite difference (FD) or finite element (FE) methods. The second step involves integrating the resulting system of semi-discrete ordinary differential equations (ODEs) in the initial value variable wrt to time, \( t \).
As an example of the MOL, Wouwer et al [5] utilize the linear advection equation to demonstrate the process. \[ \dfrac{\partial u}{\partial t} = -v \dfrac{\partial u}{\partial x} \] To begin, the equation is discretized in the spatial realm of \( x \) into an \( N \) number of grid points which are spaced evenly by the distance \( \delta x \). The spatial derivative, \( \partial u/ \partial x \), is then approximated by its second order centered FD beginning at grid point \( i \) up to the maximum discretization point \( N \) so that \[ \dfrac{\partial u}{\partial x} = -v \dfrac{u_{i+1} - u_{i-1}}{2 \Delta x} + O \left( \Delta x^2 \right), \quad i = 1, 2, \cdots, N \] Then assuming a value of \( v = 1 \) and substituting into \( \partial u/\partial t = -v \partial u/\partial x \) results in the equation \[ \dfrac{\mathrm{d} u}{\mathrm{d} t} = -\dfrac{u_{i+1} - u_{i-1}}{2 \Delta x}, \quad i = 1, 2, \cdots, N \]
Wouwer et al [5] next mention that at this point a system of \( N \) ODEs are generated which can then be integrated by an already developed by a library ODE integrator. An initial condition must then be specified next at the \( N \) grid points and the false points \( u_0 \) and \( u_{N + 1} \) for \( i = 1 \) and \( i = N \). Thus, if an example of the equation is solved for two step functions separated by a time interval of \( t = 50 \) or simply a square pulse, with a spatial length of \( N =101 \) or 100 intervals with a length of \( \Delta x \), the solution exhibits oscillatory behavior as seen in the figure by Wouwer et al [5]. This oscillation is of course false and is caused by the numerics of the problem known as a numerical distortion.
Wouwer et al [5] further discuss some issues here about this problem that I feel like are good points to intake. First is a continuation of the numerical oscillation problem. Wouwer et al express the problem that the oscillations do not dissipate with an increase in grid resolution in the spatial direction \( x \) or, in other words, and increase in the number of intervals, even though the FD equation is of the second order so you would expect as \( \Delta x \) decreased the error would decrease \( O \left( \Delta x^2 \right) \). Thus, the observation is made that will a reasonable method of approximation of a linear PDE broken down into a system of ODEs is accomplished the solutions are inaccurate.
In fact, Wouwer et al [5] explain that the accuracy of the numerical solution is dependent upon the smoothness of the analytical solution. For instance, rather than the two discontinuous jumps encountered with the square wave, a “more smooth” function would be a triangular pulse where \( u\left(x,t\right) \) is continuous but \( \partial u/\partial x \) is not continuous. As shown in the figure the MOL numerical solution (dots) matches much closer with the actual solution (solid line). Finally, if the initial condition is even “smoother” such as a cosine function, then the oscillations diminish even more. Thus, if the initial condition contains non-smooth characteristics such as discontinuities, then the discontinuities spread through the time and space variables which is indicative of hyperbolic PDEs.
However, Gear’s method is also utilized by Pike et al [8]. Gear’s method as defined by Hoffman [7] was developed by Gear in 1971 [9]. Gear’s method contains much larger stability limits for a series of implicit FD equations (FDEs). The formula appears as
\[ y_{n+1} = \gamma \left[ \beta h f_{n+1} + \left( \alpha_0 y_n + \alpha_{-1} y_{n-1} + \alpha_{-2} y_{n-2} + \cdots \right)\right] \]
where k is the global order of the FDE and the coefficients \( \gamma \), \( \beta \), \( \alpha_i \left( i = 0, 1, 2, \ldots \right) \) are shown in the table from Hoffman [7].
In addition, an interesting comment from Hoffman [7] cites that the Gear FDEs are in a FORTRAN package named LSODE which came about from researchers at Lawrence Livermore National Laboratory. According to Hoffman, this package utilizes
"...an elaborate error control procedure based on using various-order Gear FDEs in conjunction with step size halving and doubling."
Additional notes from Hoffman explain that stiff ODEs contain extra issues for solutions. Usually explicit methods do not work for stiff ODEs. However, implicit methods such as the Gear method do work for stiff problems. Hoffman defines stiff ODEs as where
"...at least one eigenvalue has a large negative real part which causes the corresponding component of the solution to vary rapidly compared to the typical scale of variation displayed by the rest of the solution."
Velten [10] states that stiff ODEs pose issues since the numerical solutions may oscillate as demonstrated beforehand. Thus, small step sizes must be implemented to obtain a correct solution. Also of note is Velten’s mention of a few software packages such as Maxima and R. Velten gives another name for the Gear method as the backward differentiation formulas (BDF) method. A part of R’s odesolve package is lsoda which stands for Livermore Solver for Ordinary Differential Equations (automatic) which came about from Petzold and Hindmarsh at California’s Lawrence Livermore National Laboratory [11, 12]. The lsoda package has a unique feature in which it automatically switches between methods for stiff and nonstiff sets of ODEs which is one of the main differences from lsode. As a further side note, according to Soetaert et al [13] the package odesolve is planned to be deprecated and deSolve is the package successor. The nonstiff case utilizes the Adams method with a variable stepsize and a variable order of up to 12th order. For the stiff case of ODEs, the lsoda package utilizes the BDF method with a variable stepsize and a variable order of up to 5th order.
In order to answer the question of stiff ODEs, let's look at an example in A First Course in the Numerical Analysis of Differential Equations by Iserles [14].
Hoffman [7] states that stiffness appears for single linear and nonlinear ODEs, higher-order linear and nonlinear ODEs, and systems of linear and nonlinear ODEs. He lists several definitions for stiffness:
Hoffman [7] states that stiffness appears for single linear and nonlinear ODEs, higher-order linear and nonlinear ODEs, and systems of linear and nonlinear ODEs. He lists several definitions for stiffness:
1. An ODE is stiff if the step size required for stability is much smaller than the step size required for accuracy.
2. An ODE is stiff if it contains some components of the solution that decay rapidly compared to other components of the solution.
3. A system of ODEs is stiff if at least one eigenvalue of the system is negative and large compared to the other eigen values of the system.
4. From a practical point of view, an ODE is stiff if the step sixe based on cost (i.e., computational time) is too large to obtain an accurate (i.e., stable) solution.
Hoffman [7] also gives a couple of examples.
Also, since it is mentioned let’s talk about Adams methods. According to Iserles [14],
In progress...to be continued.
References:
[1] IMSL Numerical Libraries. 07-23-2011, http://en.wikipedia.org/wiki/IMSL Numerical Libraries
[2] IMSL R Numerical Libraries. imsl-numerical-libraries.aspx 07-23-2011, http://www.roguewave.com/products/
[3] Visual Numerics IMSL Fortran Library User’s Guide Math Library Volume 2 of 2 - Mathematical Functions in Fortran. 07-23-2011, http://www.absoft.com/Support/Documentation/MathV2.pdf, 2003
[4] Visual Numerics IMSL Fortran Numerical Library User’s Guide Math Library Version 7.0. 07-23-2011, http://www.roguewave.com/portals/0/products/imsl-numerical-libraries/fortran-library/docs/7.0/math/math.pdf, 2010
[5] A. Vande Wouwer, P. Saucez, & W. E. Schiesser. Chapter 1 Introduction. A. Vande Wouwer, P. Saucez, & W. E. Schiesser (editors). Adaptive Method of Lines. Chapman & Hall/CRC, Boca Raton, FL. 2001
[6] A. Vande Wouwer, P. Saucez, & W. E. Schiesser (editors). Adaptive Method of Lines. Chapman & Hall/CRC, Boca Raton, FL. 2001
[7] J. D. Hoffman. Numerical Methods for Engineers and Scientists. 2 edition. Marcel Dekker, Inc., New York, NY. 2001
[8] P. Pike, C. Parigger, R. Splinter, and P. Lockhart. Temperature distribution in dental tissue after interaction with femtosecond laser pulses. Applied Optics, Volume 46, Number 34, December 2007
[9] C. W. Gear. Numerical Initial Value Problems in Ordinary Differential Equations, Prentice-Hall, Englewood Cliffs, New Jersey. 1971
[10] K. Velten. Mathematical Modeling and Simulation: Introduction for Scientists and Engineers, Wiley-VCH, Weinheim, Germany. 2009
[11] A. C. Hindmarsh. ODEPACK, a systematized collection of ODE solvers, Scientific Computing, North-Holland, Amsterdam, The Netherlands, pp. 55–64. 1983
[12] L. R. Petzold. Automatic selection of methods for solving stiff and nonstiff systems of ordinary differential equations. SIAM Journal on Scientific and Statistical Computing, 4, 136–48. 1983
[13] K. Soetaert, T. Petzoldt, and R. W. Setzer. Solving Differential Equations in R: Package deSolve. Journal of Statistical Software, 33, 4, February 2010
[14] A. Iserles. A First Course in the Numerical Analysis of Differential Equations. (2nd ed.).
Cambridge University Press, Cambridge, UK. 2009
Additional keywords:
finite difference equations (FDEs), Gear's method, LSODE, LSODA, Adams method, deSolve, R, Maxima, backward differentiation formulas (BDF) method, International Mathematics and Statistics Library (IMSL), Rogue Wave Software, DMOLCH, MOLCH, Fortran, Fortran 90, MMOLCH, Fortran 77, S MOLCH, D MOLCH, S MMOLCH, D MMOLCH, Method of Lines (MOL), Partial Differential Equations (PDEs), Finite Difference (FD), Finite Element (FE), ordinary differential equations (ODEs)
Wednesday, August 24, 2011
RKWard - another GUI for R
RKWard - http://rkward.sourceforge.net/
One of the main differences between R Commander and RkWard is that RKWard is KDE based and developed.
http://sourceforge.net/projects/rkward/
KDE Science: Thomas Friedrichsmeier on RKWard, Toolkits and the KDE Platform - 2010 13 Sep - By: Luca Beltrame - http://dot.kde.org/2010/09/13/kde-science-thomas-friedrichsmeier-rkward-toolkits-and-kde-platform
A review of a bunch of R GUIs:
R GUIs · 06/05/2010 - http://www.nettakeaway.com/tp/R/137/r-guis
One of the main differences between R Commander and RkWard is that RKWard is KDE based and developed.
RKWard aims to become an easy to use, transparent frontend to R, a powerful system for statistical computation and graphics. Besides a convenient GUI for the most important statistical functions, future versions will also provide seamless integration with an office-suite.
http://sourceforge.net/projects/rkward/
KDE Science: Thomas Friedrichsmeier on RKWard, Toolkits and the KDE Platform - 2010 13 Sep - By: Luca Beltrame - http://dot.kde.org/2010/09/13/kde-science-thomas-friedrichsmeier-rkward-toolkits-and-kde-platform
A review of a bunch of R GUIs:
R GUIs · 06/05/2010 - http://www.nettakeaway.com/tp/R/137/r-guis
Labels:
Math Software,
Numerical software
Monday, August 22, 2011
Sage: Open Source Mathematics Software
Once I get the hang of Maxima I think I will give this a go again. This can call software such as Maxima, Octave, etc.
Sage: Open Source Mathematics Software
Link to introductory videos on Sage and Python from the Sage website:
Screencasts and Videos - http://sagemath.org/help-video.html
Link to help and documentation from the Sage site:
http://sagemath.org/help.html
Sage: Open Source Mathematics Software
Sage is a free open-source mathematics software system licensed under the GPL. It combines the power of many existing open-source packages into a common Python-based interface.
Mission: Creating a viable free open source alternative to Magma, Maple, Mathematica and Matlab
Link to introductory videos on Sage and Python from the Sage website:
Screencasts and Videos - http://sagemath.org/help-video.html
Link to help and documentation from the Sage site:
http://sagemath.org/help.html
Labels:
Math,
Math Software,
Numerical math,
Numerical software,
Sage
Xmaxima
Xmaxima is a graphical interface for Maxima, written in Tcl/Tk. It also provides the openmath plotting program for Maxima, which can do some of the plots done by Maxima's default plotter (gnuplot) and a few more that gnuplot cannot do.
This manual was written for version 5.11.0 of Xmaxima. Some familiarity with Maxima 5.11.0 is assumed. There is a separate reference manual for Maxima, which can be browsed and studied from Xmaxima.
This is apparently installed by default when you install Maxima from the USC.
Xmaxima Manual: Top
Labels:
Maxima,
Numerical math,
Numerical software,
Xmaxima
Saturday, August 20, 2011
wxMaxima - Community Ubuntu Documentation - Installing the latest version by compiling and PPA
In order to install the latest wxMaxima (a Mathematica type software) by compiling the source code yourself follow these instructions (this is not necessary as you can use the PPA that I provide further below). The Ubuntu SC only installs 0.8.5 while the latest version as of this date is 11.8.0
wxMaxima - Community Ubuntu Documentation
Download the latest version here: http://sourceforge.net/projects/wxmaxima/files/
Uninstall the old version if you have one.
Then:
After
I have found the PPA for wxMaxima here -> Maxima and wxMaxima by István Blahota - https://launchpad.net/~blahota/+archive/wxmaxima as ppa:blahota/wxmaxima.
Thus to install via PPA:
Then install from USC (Ubuntu Software Center) or if an older version is already installed simply type into the terminal command line:
Links to Maxima and wxMaxima:
Maxima, a Computer Algebra System - http://maxima.sourceforge.net/
Some screen shots from the Maxima site:
Xmaxima 5.18 running on Linux (with Tk 8.5) with the Embedded plot windows option:
Xmaxima running on Windows:
Maxima running in GNU Emacs:
Maxima 5.18 running in command line mode in Linux:
Maxima running in GNU TeXmacs:
Maxima running in GNU Emacs with Imaxima mode:
Maxima Documentation - http://maxima.sourceforge.net/documentation.html
wxMaxima - http://andrejv.github.com/wxmaxima/
Some screen shots from wxMaxima:
wxMaxima on Linux:
wxMaxima on Mac OS X:
Some interesting links from the Maxima website:
wxMaxima - Community Ubuntu Documentation
Download the latest version here: http://sourceforge.net/projects/wxmaxima/files/
Uninstall the old version if you have one.
sudo apt-get remove maxima-doc wxmaxima
Then:
You will need the virtual package "build-essential" for making the package and the package "checkinstall" for building a debian package. So if you don't have it or are unsure,
sudo apt-get install build-essential checkinstall
Now its time to extract, configure, make and install your package:
tar xfvz /"locationof"/wxMaxima-"latest-version".tar.gz
sudo apt-get build-dep wxmaxima
cd /"locationof"/wxMaxima-"latest-version"/
./configure --enable-dnd --enable-printing --enable-unicode-glyphs --prefix=/usr --exec-prefix=/usr
make
sudo checkinstall
After
sudo apt-get build-dep wxmaximaI extracted the .tar.gz file because the /"locationof"/wxMaxima-"latest-version"/ directory didn't exist until you do this. You may be able to do this (extract) earlier. Then follow the rest of the directions:
ay "yes" to create a document package and paste the description of Maxima off of the website pasted bellow:
wxMaxima is a cross platform GUI for the computer algebra system maxima based on wxWidgets.
When this is done type "0" then "ENTER" and enter your email address so that people know who you are if they use your package you@somewhere as an example
hit "ENTER" and hope for the best. Checkinstall attempts to build you a deb package which it automatically installs by default and is also included in the directory you made WxMaxima, i.e. the deb is in /"locationof"/WxMaxima-"latest-version"/. Thus if everything goes smoothly you now have the latest version of wxmaxima installed.
I have found the PPA for wxMaxima here -> Maxima and wxMaxima by István Blahota - https://launchpad.net/~blahota/+archive/wxmaxima as ppa:blahota/wxmaxima.
Thus to install via PPA:
sudo add-apt-repository ppa:blahota/wxmaxima
sudo apt-get update
Then install from USC (Ubuntu Software Center) or if an older version is already installed simply type into the terminal command line:
sudo apt-get upgrade
Links to Maxima and wxMaxima:
Maxima, a Computer Algebra System - http://maxima.sourceforge.net/
Maxima is a system for the manipulation of symbolic and numerical expressions, including differentiation, integration, Taylor series, Laplace transforms, ordinary differential equations, systems of linear equations, polynomials, and sets, lists, vectors, matrices, and tensors. Maxima yields high precision numeric results by using exact fractions, arbitrary precision integers, and variable precision floating point numbers. Maxima can plot functions and data in two and three dimensions.
The Maxima source code can be compiled on many systems, including Windows, Linux, and MacOS X. The source code for all systems and precompiled binaries for Windows and Linux are available at the SourceForge file manager.
Maxima is a descendant of Macsyma, the legendary computer algebra system developed in the late 1960s at the Massachusetts Institute of Technology. It is the only system based on that effort still publicly available and with an active user community, thanks to its open source nature. Macsyma was revolutionary in its day, and many later systems, such as Maple and Mathematica, were inspired by it.
The Maxima branch of Macsyma was maintained by William Schelter from 1982 until he passed away in 2001. In 1998 he obtained permission to release the source code under the GNU General Public License (GPL). It was his efforts and skill which have made the survival of Maxima possible, and we are very grateful to him for volunteering his time and expert knowledge to keep the original DOE Macsyma code alive and well. Since his passing a group of users and developers has formed to bring Maxima to a wider audience.
We are constantly updating Maxima, to fix bugs and improve the code and the documentation. We welcome suggestions and contributions from the community of Maxima users. Most discussion is conducted on the Maxima mailing list.
Some screen shots from the Maxima site:
Xmaxima 5.18 running on Linux (with Tk 8.5) with the Embedded plot windows option:
Xmaxima running on Windows:
Maxima running in GNU Emacs:
Maxima 5.18 running in command line mode in Linux:
Maxima running in GNU TeXmacs:
Maxima running in GNU Emacs with Imaxima mode:
Maxima Documentation - http://maxima.sourceforge.net/documentation.html
wxMaxima - http://andrejv.github.com/wxmaxima/
About
wxMaxima is a document based interface for the computer algebra system Maxima. wxMaxima uses wxWidgets and runs natively on Windows, X11 and Mac OS X. wxMaxima provides menus and dialogs for many common maxima commands, autocompletion, inline plots and simple animations. wxMaxima is distributed under the GPL license.
Some screen shots from wxMaxima:
wxMaxima on Linux:
wxMaxima on Mac OS X:
Some interesting links from the Maxima website:
Related Projects
Stand-alone user interfaces for Maxima
Imaxima and imath
Developers: Jesper Harder, Yasuaki Honda.
“Imaxima.el provides support for interacting with the computer algebra system Maxima in an Emacs buffer. Imaxima processes the output from Maxima with TeX and inserts the resulting image in the buffer.”
→ http://sites.google.com/site/imaximaimath/
Kayali
Developer: Abdulhaq Lynch.
“Kayali is a Qt based Computer Algebra System (CAS) that can also be used as an advanced replacement for KDE KCalc. It is essentially a front end GUI for Maxima (and is easily extended to other CAS back-ends) and Gnuplot.”
→ http://kayali.sourceforge.net/
LyX
There is a way to send commands to Maxima from the LyX document processor. It's somewhat different from the TeXmacs functionality, but does seem to be functional at least on a basic level.
See an example document: http://maxima.sourceforge.net/lyx+maxima.lyx.
→ http://www.lyx.org/
Symaxx2
Developer: Markus Nentwig.
“Symaxx is a graphical front end for the Maxima computer algebra system (GPL).”
→ http://symaxx.sourceforge.net/
TeXmacs
Developer: Joris van der Hoeven.
“GNU TeXmacs is a free wysiwyw (what you see is what you want) editing platform with special features for scientists. The software aims to provide a unified and user friendly framework for editing structured documents with different types of content (text, graphics, mathematics, interactive content, etc.).”
→ http://www.texmacs.org/
wxMaxima
Developers: Andrej Vodopivec et al
“wxMaxima is a cross platform GUI for the computer algebra system maxima based on wxWidgets. It provides menu and dialog based interface for maxima and a nice display of math output.”
→ http://wxmaxima.sourceforge.net/
Web interfaces running Maxima
Calc.Matthen.com
Online integrator, differentiator, graph plotter, etc.
→ http://calc.matthen.com/
Interactive Demos of Mathematical Computations
(Institute for Computational Mathematics at Kent State U)
→ http://icm.mcs.kent.edu/research/demo.html
Mathematical Assistant
Developers: Robert Marik, Miroslava Tihlarikova.
“This site contains interface to access computer algebra system Maxima and automatically solve selected typical problems from mathematical courses, including intermediate steps in the solution.”
Mathassistant project page at Sourceforge.
→ http://user.mendelu.cz/marik/maw/index.php?lang=en
Maxima-Online
Developer: Piotr Lewalski
“Maxima-Online is a web based front end to the oryginal Maxima command line program. It's task is to deliver an interface which is simple and easy to use.”
→ http://maxima-online.lewalski.pl/
MaximaPHP
Developer: Bowo Prasetyo
“A PHP program to access Maxima on the server interactively from a website.”
See also: Maxima show-case.
See also: MaximaPHP project page at SourceForge.
→ http://www.my-tool.com/mathematics/maximaphp/
WebMathematics Interactive
Developer: Zoltan Kovacs, U Szeged, Hungary.
WMI On-line demo
Documentation (including 3 short movies in English and 3 in Hungarian)
Old version
Details of development (obsolete)
→ http://wmi.math.u-szeged.hu/wmi/math.php
Systems using Maxima as a component in a larger scheme
Euler
Developer: Rene Grothmann.
“Euler is a MatLab like numerical system with a GUI frontend in notebook style ala Maple, plot features, and a numerical programming language. Euler can be used as a GUI frontend to Maxima. It can also exchange data and expressions with Maxima, helping Maxima with numerical calculations, and Euler with symbolic evaluation.”
→ http://mathsrv.ku-eichstaett.de/MGF/homes/grothmann/euler/
GeoGebraCAS
Developer: Markus Hohenwarter et al.
“GeoGebra is free and multi-platform dynamic mathematics software for all levels of education that joins geometry, algebra, tables, graphing, statistics and calculus in one easy-to-use package. GeoGebraCAS extends the Computer Algebra System (CAS) features of GeoGebra to allow students to work with fractions, equations, and formulas that include variables.”
→ http://www.geogebra.org/trac/wiki/GeoGebraCAS/Documentation
The LearningOnline Network with CAPA
Developer: Gerd Kortemeyer.
“Sharing and using online learning and assessment materials across institutions and disciplines.”
Computer Algebra System (notes about integration of Maxima with LON-CAPA).
→ http://www.lon-capa.org/
MathDrag'n
Developer: James Hart.
MathDrag'n project page at SourceForge.
“MathDrag'n is an interface designed to help you, the user, maintain almost complete control over the algebra while stopping you from making mistakes. In contrast to most computer algebra systems, MathDrag'n's philosophy is that the user interface is first, and that ease of use is what you want.”
→ http://mathdragn.squarespace.com/
Mediawiki Algebra extension
Developer: Markus Arndt.
“defines a maxima session. Any line terminating with a semicolon is passed to maxima for evaluation. For all other lines the wiki syntax applies.”
→ http://meta.wikimedia.org/wiki/User:Mafs/Computer_algebra
SAGE
“Sage is a comprehensive open-source mathematics software suite that has the mission statement ‘Creating a viable free open source alternative to Magma, Maple, Mathematica, and Matlab.’”
SAGE web interface.
→ http://sagemath.org/
STACK
Developer: Chris Sangwin, U Birmingham, UK.
STACK SourceForge project page.
→ http://www.stack.bham.ac.uk/
WIMS
→ http://wims.unice.fr/wims/en_home.html
Third Party Code
There are some packages we cannot include in the official Maxima distribution due to legal restrictions or because they are not in a stable state yet.
If you know any old Macsyma code still available on the Internet or new Maxima packages that should be included in this list, please tell us about it so we can add a link or even add it to the official distribution, if its license is compatible with Maxima's.
A collection of user-contributed code
Misc code by Willy Hereman et. al.
A series of interesting Macsyma packages. Commercial use is not permitted without consent of the authors.
Pw.mac
The package pw.mac extends Maxima by enabling it to work with piecewise continuous functions.
Qinf (quantum information and entanglement package)
A quantum information package that allows the manipulation of instances of objects — operators, vectors, tensors, etc. — that appear in the theory of quantum information and quantum entanglement.
SymSAP
Symbolic matrix analysis of structures. SymSAP aims to become a powerful didactic tool to help students learn structural analysis.
rfMaxima
rfMaxima allows for symbolic derivation, as well as numerical evaluation (incl. Bode and Smith chart plotting), of 2-port network (ABCD, G, InverseABCD, H, S, Y, and Z), noise and stability parameters. Derivations are based on the solution of the set of Kirchoff current and voltage law equations representing the 2-port. Expressions can be exported to HTML or TeX. Figures can be exported to EPS or PNG.
Other Open Source Computer Algebra Systems
Axiom
“Axiom is a general purpose Computer Algebra system. It is useful for doing mathematics by computer and for research and development of mathematical algorithms. It defines a strongly typed, mathematically correct type hierarchy. It has a programming language and a built-in compiler.”
There is also an interesting Rosetta Stone which offers translations of many basic operations for several computer algebra systems, including Maxima.
→ http://axiom-developer.org/
GAP
“GAP is a system for computational discrete algebra, with particular emphasis on Computational Group Theory.”
→ http://turnbull.mcs.st-and.ac.uk/~gap/
Jasymca
“Jasymca is a symbolic calculator written for mobile phones and PDAs. It solves and manipulates equations, handles basic calculus problems, and provides a few more typical functions of computer algebra systems. The syntax is loosely related to GNU-Maxima.”
→ http://webuser.hs-furtwangen.de/~dersch
REDUCE
“REDUCE is an interactive system for general algebraic computations of interest to mathematicians, scientists and engineers.”
→ http://reduce-algebra.com
SINGULAR
“SINGULAR is a Computer Algebra System for polynomial computations with special emphasis on the needs of commutative algebra, algebraic geometry, and singularity theory.”
→ http://www.singular.uni-kl.de/
Yacas
“YACAS is an easy to use, general purpose Computer Algebra System, a program for symbolic manipulation of mathematical expressions. It uses its own programming language designed for symbolic as well as arbitrary-precision numerical computations.”
→ http://yacas.sourceforge.net/
Other Open Source Mathematical Software
Oberwolfach References on Mathematical Software: http://orms.mfo.de/
Free mathematical and computational software directory: http://cadadr.org/fm/
ARIBAS
“ARIBAS is an interactive interpreter for big integer arithmetic and multi-precision floating point arithmetic with a Pascal/Modula like syntax. It has several builtin functions for algorithmic number theory like gcd, Jacobi symbol, Rabin probabilistic prime test, factorization algorithms (Pollard rho, elliptic curve, continued fraction, quadratic sieve), etc.”
→ http://www.mathematik.uni-muenchen.de/~forster/sw/aribas.html
NumPy
“The fundamental package needed for scientific computing with Python is called NumPy. This package contains a powerful N-dimensional array object, sophisticated (broadcasting) functions, tools for integrating C/C++ and Fortran code, and useful linear algebra, Fourier transform, and random number capabilities.”
→ http://numpy.scipy.org/
Octave
“GNU Octave is a high-level language, primarily intended for numerical computations. It provides a convenient command line interface for solving linear and nonlinear problems numerically, and for performing other numerical experiments using a language that is mostly compatible with Matlab.”
→ http://www.gnu.org/software/octave/
PARI/GP
“PARI/GP is a widely used computer algebra system designed for fast computations in number theory (factorizations, algebraic number theory, elliptic curves...), but also contains a large number of other useful functions to compute with mathematical entities such as matrices, polynomials, power series, algebraic numbers etc., and a lot of transcendental functions.”
→ http://pari.math.u-bordeaux.fr/
R
“R is a free software environment for statistical computing and graphics. It compiles and runs on a wide variety of UNIX platforms, Windows and MacOS.”
→ http://www.r-project.org/
Information about Computer Algebra Systems
List of computer algebra systems (Wikipedia)
Lots of links there.
→ http://en.wikipedia.org/wiki/List_of_computer_algebra_systems
SymbolicNet
A very good starting point to learn about symbolic computation and computer algebra systems.
→ http://www.symbolicnet.org/
Friday, August 12, 2011
The R Project for Statistical Computing
I thought I had posted something about the math software R, but I guess I haven't. I already posted something on R-Commander, a GUI for R.
The R Project for Statistical Computing
Screenshot:
The R Manuals - http://cran.r-project.org/manuals.html
R Documentation - http://www.r-project.org/other-docs.html
The R Project for Statistical Computing
Introduction to R
R is a language and environment for statistical computing and graphics. It is a GNU project which is similar to the S language and environment which was developed at Bell Laboratories (formerly AT&T, now Lucent Technologies) by John Chambers and colleagues. R can be considered as a different implementation of S. There are some important differences, but much code written for S runs unaltered under R.
R provides a wide variety of statistical (linear and nonlinear modelling, classical statistical tests, time-series analysis, classification, clustering, ...) and graphical techniques, and is highly extensible. The S language is often the vehicle of choice for research in statistical methodology, and R provides an Open Source route to participation in that activity.
One of R's strengths is the ease with which well-designed publication-quality plots can be produced, including mathematical symbols and formulae where needed. Great care has been taken over the defaults for the minor design choices in graphics, but the user retains full control.
R is available as Free Software under the terms of the Free Software Foundation's GNU General Public License in source code form. It compiles and runs on a wide variety of UNIX platforms and similar systems (including FreeBSD and Linux), Windows and MacOS.
The R environment
R is an integrated suite of software facilities for data manipulation, calculation and graphical display. It includes
- an effective data handling and storage facility,
- a suite of operators for calculations on arrays, in particular matrices,
- a large, coherent, integrated collection of intermediate tools for data analysis,
- graphical facilities for data analysis and display either on-screen or on hardcopy, and
- a well-developed, simple and effective programming language which includes conditionals, loops, user-defined recursive functions and input and output facilities.
- The term "environment" is intended to characterize it as a fully planned and coherent system, rather than an incremental accretion of very specific and inflexible tools, as is frequently the case with other data analysis software.
R, like S, is designed around a true computer language, and it allows users to add additional functionality by defining new functions. Much of the system is itself written in the R dialect of S, which makes it easy for users to follow the algorithmic choices made. For computationally-intensive tasks, C, C++ and Fortran code can be linked and called at run time. Advanced users can write C code to manipulate R objects directly.
Many users think of R as a statistics system. We prefer to think of it of an environment within which statistical techniques are implemented. R can be extended (easily) via packages. There are about eight packages supplied with the R distribution and many more are available through the CRAN family of Internet sites covering a very wide range of modern statistics.
R has its own LaTeX-like documentation format, which is used to supply comprehensive documentation, both on-line in a number of formats and in hardcopy.
Screenshot:
The R Manuals - http://cran.r-project.org/manuals.html
R Documentation - http://www.r-project.org/other-docs.html
Labels:
Numerical math,
Numerical software,
R
Wednesday, August 10, 2011
R Commander: A Basic-Statistics GUI for R
R Commander
Screenshot from the site:
From the website:
Screenshot from the site:
From the website:
For more details, see my paper on the R Commander in the Journal of Statistical Software.
The R-Commander GUI consists of a window containing several menus, buttons, and information fields. (The menu tree, etc., are shown below.) In addition, the Commander window contains script and output text windows. The R-Commander menus are easily configurable through a text file or, preferably, through plug-in packages.
The menus lead to simple dialog boxes, the general contents of which are more or less obvious from the names of the menu items. These boxes have a common structure, including a help button leading to the help page for a relevant function.
By default, commands generated via the dialogs are posted to the output window, along with printed output, and to the script window. Lines in the script window can be edited and (re)submitted for execution. Error messages, warnings, and "notes" appear in a messages window.
Commands access a current or active data set (data frame). When a new data set is read (from an attached package or imported), it becomes the active data set. The user can also select an active data set from among data frames currently in memory.
In addition to standard packages, the Commander uses functions in a number of other packages: abind, aplpack, car, colorspace, effects, Hmisc, leaps, lmtest, multcomp, relimp, rgl, and (on Windows) RODBC. To install the Rcmdr package along with all of these and their dependencies, use the command install.packages("Rcmdr", dependencies=TRUE). If any of these packages are missing, the Rcmdr will offer to install them when it starts up. Note: These other packages also have dependencies, which have dependencies, etc., so many packages get installed; with a fast Internet connection, the process should go reasonably quickly, however.
My object in designing and implementing this GUI was to cover the content of a basic-statistics course. The target text was Moore's The Basic Practice of Statistics, Second Edition (Freeman, 2000), which is the text that I used for a two-semester introduction to statistics for undergraduate sociology majors. The R Commander implements the content of this text plus some additional material (e.g., linear and generalized linear models). As a result of several suggestions that I have received, the coverage is now larger than originally envisaged.
I must confess that I'm not terribly enamored of menu/dialog box interfaces to statistical software, but I do feel that these interfaces have a role for introductory and occasional use. The Commander interface is not innovative, but I hope that it's simple and familiar. One of my design goals was to wean users from the GUI to writing commands, which is one motivation for the script window.
It is relatively easy for me to add statistical functionality to the R Commander, and I'd appreciate suggestions for what you'd like to see implemented. Please remember, however, that my intention is to keep things simple and basic. In particular, I don't like extensive menu/dialog-box interfaces to large statistical systems that attempt to provide access to every option and procedure. In R, of course, which relies on hundreds of contributed packages, this is not feasible anyway. As mentioned, the R Commander can also be extended by plug-in packages: See my article in the December 2007 issue of R News.
I'm making the GUI available as the Rcmdr package. You can get a copy of the latest released version of the Rcmdr package through CRAN. I should mention that I've only tested the package under Windows 95, 2000, XP; Vista (recent versions under Vista), and under Ubuntu Linux (earlier versions under Red Hat and Quantian Linux); and under Mac OS X. Mac OS X users in particular should see the installation notes.
The lastest version of the Rcmdr has some new features, and there are many new features beyond the original release. (See the CHANGES file in the installed or source package for details.) Version 0.9-9 introduced substantial changes to the interface, with output by default routed to an output window within the main Commander window; version 0.9-10 included rewritten dialog-box generating functions, reducing the R code for the package by about 40 percent. Development version 0.9-18 (never submitted to CRAN) introduced other substantial changes, such as conditionally activated menus. Version 1.0-0 was the first "non-beta" version. Version 1.1-1 included support for translation into other languages, using the tools for internationalization and localization introduced in R 2.1.0; please contact me if you'd like to contribute a translation of the Rcmdr package into another language. Version 1.3-0 introduced "plug-ins," which simplify extending the R Commander: See ?Plugins. There are now a number of plug-in packages on CRAN, most with names of the form RcmdrPlugin.* (e.g., RcmdrPlugin.survival).
An introductory manual (in a PDF file, up-to-date as of Rcmdr version 1.6-0) is part of the R Commander package and is accessible from its Help menu. A Spanish translation of the help page for the Commander has been generously contributed by Manuel Muñoz Márquez.
I'd very much appreciate learning about your experiences.
Labels:
Math,
Numerical math,
Numerical software,
R,
R commander
Visual Numerics, Inc. IMSL® Fortran Numerical Math Library
Here is the link to the Visual Numerics, Inc. IMSL® Fortran Numerical Math Library online document.
Visual Numerics, Inc. IMSL® Fortran Numerical Math Library Online Document
Visual Numerics, Inc. IMSL® Fortran Numerical Math Library Online Document
The IMSL MATH LIBRARY is a collection of Fortran routines and functions useful in mathematical analysis research and application development. Each routine is designed and documented for use in research activities as well as by technical specialists.
© 1970-2007 Visual Numerics, IMSL and PV-WAVE are registered trademarks of Visual Numerics, Inc. in the U.S. and other countries. JMSL, JWAVE, TS-WAVE and Knowledge in Motion are trademarks of Visual Numerics, Inc. All other company, product or brand names are the property of their respective owners.
IMPORTANT NOTICE: Information contained in this documentation is subject to change without notice. Use of this document is subject to the terms and conditions of a Visual Numerics Software License Agreement, including, without limitation, the Limited Warranty and Limitation of Liability. If you do not accept the terms of the license agreement, you may not use this documentation and should promptly return the product for a full refund. This documentation may not be copied or distributed in any form without the express written consent of Visual Numerics.
Labels:
Fortran,
Numerical math,
Numerical software
Sunday, July 24, 2011
Some thoughts on numerical software and the scientist and some info on libMesh, OctMesh
I am slowly delving into the world of open source alternatives to mathematical software. Partially because I am taking a numerical PDE course and working on the assigned problems in the class and partially because of general interest. My computer and programming skills, I would say are at a general low level knowledge base and skills. That is, I know a bit about a medium range of stuff from classes and picking up things from my environment (colleagues, my own investigations, etc.)
I think it is important as scientists and engineers to not only be able to use these software but also have some idea of what is happening in the black box. Of course depending on the situation and interest level, just running the software and not caring how or why may be necessary.
Many of the topics and materials are over my head, especially the programming based material. I mean I have some inkling because I am pretty capable at utilizing MATLAB/Octave type m-files to program a routine, but the deeper stuff I am trying to learn. Yeah, we had a intro to C program class in undergrad, but unless you use it frequently and somewhat indepthly then you're going to forget the little you knew, especially at a younger age when you may not realize the importance of it.
I feel like it is imperative that scientists and engineers in my field at a PhD level should be well equipped to deal with numerics and computers since we are involved with them in not only our everyday tasks but also, more than likely, our scientific endeavors. You almost should have or need a computer science degree as well if you want to under things a bit better. It doesn't have to be a literal degree either, you can do a majority of research and teaching to yourself like I am attempting, :P.
However, one problem with the computational sciences is that there is an immense gorge of knowledge to explore. That is, there are several languages in use which in turn use there own format even if algorithm structure doesn't change between languages for a routine (that is, say for example to program a Runge-Kutta solver you would take the same or very similar steps, but the input and commands might and probably will differ; also most software comes with packages which probably have a Runge-Kutta function of some sort. I was just giving an example which is a probable problem in a numerical mathematics class). Some languages are used more often in certain areas or are for specific goals while others are more popular among groups. For example, engineers may be more comfortable with a MATLAB/Octave base software while others more inclined in the CS may use C++, Fortran, or Python. Another example involves antiquity. It is my feeling that Fortran is pretty old and not favorable among newer programmers while Python seems to be the new guy in town over C++, Java, etc. Code also varies for purposes such as LaTeX code for document typesetting and HTML code for website development.
Another area of vastness is the differences in operating systems that computers use. The big three are Microsoft Windows, the Mac OS (not even sure what it is called) based on Unix, and Linux OSs such as Ubuntu, Fedora, etc. Now in most cases, when in MS Windows you probably won't use the command line too often if ever and the same goes for Mac since they are largely based on GUIs with the users. Now you may have to know a few tricks here and there such as pointing something to a path name and such depending on your activities. I mean, I really don't even know much about that as well. Mac OS is based on UNIX which is closely related to the Linux kernel, but I am not sure about this either??!? Linux is based on command line interfaces but has plenty of friendly GUI based distros. I guess Linux is more accessible to the guts of the software code which it should be since it is open source. In Linux you are probably going to have to use the command line eventually (like me) because you'll need to get into the guts to make some things work (one bad thing about open source) to implement someone's work for a fix (the good thing about open source). For example, say setting up a quad display for four monitors is apparently a little more difficult or labor intensive than Windows which I have heard works fine (I am working on this, more later). My point is that you may run into deeper stuff when dealing with OSs instead of the common and general surfacey use of the GUI at a somewhat blindly method for everyday usage. That is, grandma can probably read and write email while the grandson can setup a contact list and chat using messenger and Outlook or Thunderbird. Grandma isn't going to care much about anything else, she just wants to check facebook while the grandson will be more open to and exposed more to the deep computer world even if it only goes as deep as Outlook/Thunderbird.
Finally, a difference exists between mathematical software and general programming too. Say in Mathematica, you can probably "program" it to check your derivative, plot some graphs, and generate a matrix of data (say velocity on an r,z map). It's pretty simple once you learn the commands, but you can also delve deeper into the guts (I don't really know an example right now, :\). The same goes for MATLAB. As I've said before, most software comes with packages built in so the user doesn't have to worry about starting from scratch. This is what I like about MATLAB. It is less intensive than say a more "naked" approach such as C++. This also makes it more friendly to less technologically inclined users reaching a further and bigger audience. Say, a middle school teacher. Plus, you are not going to start from scratch in C++ writing a program to solve an equation unless it is an assignment, you are investigating a new approach, or you are simply just interested.
So, trying to reel it in now, the post was originally about some open source software which I was going to provide a brief explanation and a link to. But, I feel like this is relevant and it is the purpose of this blog. Eventually, I hope to post more examples and video of how to use all of this software and computer junk! This blog will help me keep things somewhat organized and at the same time develop a list/source for quick reference for others to enjoy if they like (I also have a wiki-website which will help organize material better while the blog will alert those who care about new post, however, I have not kept up with the webiste, maybe one day!). I know I learn better and more quickly to some extend by short examples. I then can built off those. However, for the open source software material and support are sometimes hard to come by! For example, I am trying to solve a simple PDE for my numerical class, but I am learning a new software, Octave. Octave is very similar to MATLAB, but doesn't have as much development as MATLAB. The good thing there are people, like me, who want to use open source and who are more skilled at development (unlike me) will contribute to making a package, software support, etc. For example, say Octave doesn't have the exact package like MATLAB for pdes. Someone can jump in and develop a similar package or one that might be a different technique works just as well. Many open source projects have mailing lists for updates, bugs, and releases and also things to be done or suggestions. For example, the Octave-Forge site has links for the extra packages for GNU Octave, developers, documentation, FAQ, bugs, mailing lists, etc.
Also, there are a few programs out there that will get the same goals accomplished. For instance, supposedly SciLab will accomplish MATLAB tasks, but I think it has a little different structure than the MATLAB/Octave type. So not only do you have choices you also have learning curves. For example, right now I am struggling with learning some Mathematica and MATLAB open source replacements, but once I learn them, I will be that much better later on. You may have to do some investigation, but that is what research and science is all about. Of course you should moderate yourself so you are productive and efficient. I will try to keep up this blog so that others may be able to learn from my endeavors. My hope is to become proficient in Mathematica type software wxMaxima/Maxima and SAGE, MATLAB type software such as Octave/QtOctave and maybe SciLab, and Origin type software such as QtiPlot and SciDavis. I also would like to learn a little about most of the programming languages by providing examples and videos of the same example say in Octave, C++, Fortran, JAVA, Python, etc. I am also hoping to become more knowledgeable in open source CFD and meshing so I won't have to rely as much on Fluent, even though Fluent is a great program but very costly! I will probably be posting examples of Fluent too.
One last thing which I have hinted at through this post. The inviting thing, and the idea that intrigue me and got me hooked, is the ability to customize and be creative and free (I know, I sound like a hippy, but hippies are bad, are they?! :P). Using open-source stuff such as Linux and LaTeX gives the user a wide range of unique outlets that you would not or rarely get with MS and their software. Of course with so many choices the user can become overwhelmed and overload on information. My advice is to pick a few things and built off that. For example, for new users to Linux I would suggest using Ubuntu. Then later on once you get a slight idea, a little grasp of what's going on, you can then begin to explore other distros if you like. The best thing to do, IMO, is to start off slow and with a few choices (2 or 3 max), maybe narrow down the choices to one, then build up gradually at your own pace, but do not let it overwhelm you so you do not become productive, then once you become comfortable, somewhat skilled, and productive you can move on or try something else if you like to see if there is something out there for you. For example, I started off with Texmaker as my LaTeX editor. I then tried Kile and really liked it. I used Kile most of the time, but would jump back to TM every now and then just to make sure I still liked Kile just a little more. I then tried Lyx, didn't like it because it was a different format even though it was based on TeX. I tried Texworks. I didn't like it because it went all weird on me one day and erased a file. I tried gedit with the LaTeX plugin and I didn't like that either. I also tried GNU TeXmacs, but I didn't like it for the same reasons as Lyx. I kept coming back to Kile, and love it. It has all the right options, it's simple, stable, and aesthetically pleasing. Although, I still might try Emacs with Auctex or the VIM editor with the LaTeX-suite. So, as you can see, my LaTeX editor serves a great example of what I am talking about and trying to convey.
So back to the original topics. I stumbled across this software called libMesh on sourceforge.net Sourceforge is a website which helps promote open source projects by hosting them for download, documentation, help, forums, etc as I mentioned earlier about Octave-Forge which is also on Sourceforge.
libMesh - C++ Finite Element Library
From the libMesh site
This is OctMesh where I found the link to libMesh.
OctMesh - J. Rafael Rodríguez Galván - February 1, 2007 - http://octmesh.forja.rediris.es/
From the website (because they can generally say it better than I can reword it!),
Again, most of this is foggy to me. I will update if I use and/or understand more. In general, I just hope maybe someone will find it useful.
I think it is important as scientists and engineers to not only be able to use these software but also have some idea of what is happening in the black box. Of course depending on the situation and interest level, just running the software and not caring how or why may be necessary.
Many of the topics and materials are over my head, especially the programming based material. I mean I have some inkling because I am pretty capable at utilizing MATLAB/Octave type m-files to program a routine, but the deeper stuff I am trying to learn. Yeah, we had a intro to C program class in undergrad, but unless you use it frequently and somewhat indepthly then you're going to forget the little you knew, especially at a younger age when you may not realize the importance of it.
I feel like it is imperative that scientists and engineers in my field at a PhD level should be well equipped to deal with numerics and computers since we are involved with them in not only our everyday tasks but also, more than likely, our scientific endeavors. You almost should have or need a computer science degree as well if you want to under things a bit better. It doesn't have to be a literal degree either, you can do a majority of research and teaching to yourself like I am attempting, :P.
However, one problem with the computational sciences is that there is an immense gorge of knowledge to explore. That is, there are several languages in use which in turn use there own format even if algorithm structure doesn't change between languages for a routine (that is, say for example to program a Runge-Kutta solver you would take the same or very similar steps, but the input and commands might and probably will differ; also most software comes with packages which probably have a Runge-Kutta function of some sort. I was just giving an example which is a probable problem in a numerical mathematics class). Some languages are used more often in certain areas or are for specific goals while others are more popular among groups. For example, engineers may be more comfortable with a MATLAB/Octave base software while others more inclined in the CS may use C++, Fortran, or Python. Another example involves antiquity. It is my feeling that Fortran is pretty old and not favorable among newer programmers while Python seems to be the new guy in town over C++, Java, etc. Code also varies for purposes such as LaTeX code for document typesetting and HTML code for website development.
Another area of vastness is the differences in operating systems that computers use. The big three are Microsoft Windows, the Mac OS (not even sure what it is called) based on Unix, and Linux OSs such as Ubuntu, Fedora, etc. Now in most cases, when in MS Windows you probably won't use the command line too often if ever and the same goes for Mac since they are largely based on GUIs with the users. Now you may have to know a few tricks here and there such as pointing something to a path name and such depending on your activities. I mean, I really don't even know much about that as well. Mac OS is based on UNIX which is closely related to the Linux kernel, but I am not sure about this either??!? Linux is based on command line interfaces but has plenty of friendly GUI based distros. I guess Linux is more accessible to the guts of the software code which it should be since it is open source. In Linux you are probably going to have to use the command line eventually (like me) because you'll need to get into the guts to make some things work (one bad thing about open source) to implement someone's work for a fix (the good thing about open source). For example, say setting up a quad display for four monitors is apparently a little more difficult or labor intensive than Windows which I have heard works fine (I am working on this, more later). My point is that you may run into deeper stuff when dealing with OSs instead of the common and general surfacey use of the GUI at a somewhat blindly method for everyday usage. That is, grandma can probably read and write email while the grandson can setup a contact list and chat using messenger and Outlook or Thunderbird. Grandma isn't going to care much about anything else, she just wants to check facebook while the grandson will be more open to and exposed more to the deep computer world even if it only goes as deep as Outlook/Thunderbird.
Finally, a difference exists between mathematical software and general programming too. Say in Mathematica, you can probably "program" it to check your derivative, plot some graphs, and generate a matrix of data (say velocity on an r,z map). It's pretty simple once you learn the commands, but you can also delve deeper into the guts (I don't really know an example right now, :\). The same goes for MATLAB. As I've said before, most software comes with packages built in so the user doesn't have to worry about starting from scratch. This is what I like about MATLAB. It is less intensive than say a more "naked" approach such as C++. This also makes it more friendly to less technologically inclined users reaching a further and bigger audience. Say, a middle school teacher. Plus, you are not going to start from scratch in C++ writing a program to solve an equation unless it is an assignment, you are investigating a new approach, or you are simply just interested.
So, trying to reel it in now, the post was originally about some open source software which I was going to provide a brief explanation and a link to. But, I feel like this is relevant and it is the purpose of this blog. Eventually, I hope to post more examples and video of how to use all of this software and computer junk! This blog will help me keep things somewhat organized and at the same time develop a list/source for quick reference for others to enjoy if they like (I also have a wiki-website which will help organize material better while the blog will alert those who care about new post, however, I have not kept up with the webiste, maybe one day!). I know I learn better and more quickly to some extend by short examples. I then can built off those. However, for the open source software material and support are sometimes hard to come by! For example, I am trying to solve a simple PDE for my numerical class, but I am learning a new software, Octave. Octave is very similar to MATLAB, but doesn't have as much development as MATLAB. The good thing there are people, like me, who want to use open source and who are more skilled at development (unlike me) will contribute to making a package, software support, etc. For example, say Octave doesn't have the exact package like MATLAB for pdes. Someone can jump in and develop a similar package or one that might be a different technique works just as well. Many open source projects have mailing lists for updates, bugs, and releases and also things to be done or suggestions. For example, the Octave-Forge site has links for the extra packages for GNU Octave, developers, documentation, FAQ, bugs, mailing lists, etc.
Also, there are a few programs out there that will get the same goals accomplished. For instance, supposedly SciLab will accomplish MATLAB tasks, but I think it has a little different structure than the MATLAB/Octave type. So not only do you have choices you also have learning curves. For example, right now I am struggling with learning some Mathematica and MATLAB open source replacements, but once I learn them, I will be that much better later on. You may have to do some investigation, but that is what research and science is all about. Of course you should moderate yourself so you are productive and efficient. I will try to keep up this blog so that others may be able to learn from my endeavors. My hope is to become proficient in Mathematica type software wxMaxima/Maxima and SAGE, MATLAB type software such as Octave/QtOctave and maybe SciLab, and Origin type software such as QtiPlot and SciDavis. I also would like to learn a little about most of the programming languages by providing examples and videos of the same example say in Octave, C++, Fortran, JAVA, Python, etc. I am also hoping to become more knowledgeable in open source CFD and meshing so I won't have to rely as much on Fluent, even though Fluent is a great program but very costly! I will probably be posting examples of Fluent too.
One last thing which I have hinted at through this post. The inviting thing, and the idea that intrigue me and got me hooked, is the ability to customize and be creative and free (I know, I sound like a hippy, but hippies are bad, are they?! :P). Using open-source stuff such as Linux and LaTeX gives the user a wide range of unique outlets that you would not or rarely get with MS and their software. Of course with so many choices the user can become overwhelmed and overload on information. My advice is to pick a few things and built off that. For example, for new users to Linux I would suggest using Ubuntu. Then later on once you get a slight idea, a little grasp of what's going on, you can then begin to explore other distros if you like. The best thing to do, IMO, is to start off slow and with a few choices (2 or 3 max), maybe narrow down the choices to one, then build up gradually at your own pace, but do not let it overwhelm you so you do not become productive, then once you become comfortable, somewhat skilled, and productive you can move on or try something else if you like to see if there is something out there for you. For example, I started off with Texmaker as my LaTeX editor. I then tried Kile and really liked it. I used Kile most of the time, but would jump back to TM every now and then just to make sure I still liked Kile just a little more. I then tried Lyx, didn't like it because it was a different format even though it was based on TeX. I tried Texworks. I didn't like it because it went all weird on me one day and erased a file. I tried gedit with the LaTeX plugin and I didn't like that either. I also tried GNU TeXmacs, but I didn't like it for the same reasons as Lyx. I kept coming back to Kile, and love it. It has all the right options, it's simple, stable, and aesthetically pleasing. Although, I still might try Emacs with Auctex or the VIM editor with the LaTeX-suite. So, as you can see, my LaTeX editor serves a great example of what I am talking about and trying to convey.
So back to the original topics. I stumbled across this software called libMesh on sourceforge.net Sourceforge is a website which helps promote open source projects by hosting them for download, documentation, help, forums, etc as I mentioned earlier about Octave-Forge which is also on Sourceforge.
libMesh - C++ Finite Element Library
From the libMesh site
The libMesh library provides a framework for the numerical simulation of partial differential equations using arbitrary unstructured discretizations on serial and parallel platforms. A major goal of the library is to provide support for adaptive mesh refinement (AMR) computations in parallel while allowing a research scientist to focus on the physics they are modeling.
libMesh currently supports 1D, 2D, and 3D steady and transient simulations on a variety of popular geometric and finite element types. The library makes use of high-quality, existing software whenever possible. PETSc is used for the solution of linear systems on both serial and parallel platforms, and LASPack is included with the library to provide linear solver support on serial machines. An optional interface to SLEPc is also provided for solving both standard and generalized eigenvalue problems.
The libMesh library has been actively developed at The University of Texas at Austin in the CFDLab since March 2002. Major contributions have come from developers at the Technische Universität Hamburg-Harburg Institute of Modelling and Computation, and recent contributions have been made by CFDLab graduates at Sandia National Laboratories and NASA Lyndon B. Johnson Space Center. The libMesh developers welcome contributions in the form of patches and bug reports (preferably with a minimal test case that reliably reproduces the error) to the official mailing lists. Many thanks to SourceForge for hosting the project. You can find out what is currently happening in the development branch by checking out the SVN Logs online, and you can see many people are downloading the library on the statistics page.
This is OctMesh where I found the link to libMesh.
OctMesh - J. Rafael Rodríguez Galván - February 1, 2007 - http://octmesh.forja.rediris.es/
From the website (because they can generally say it better than I can reword it!),
OctMesh is a toolbox for the resolution of partial differential equations (PDE) by means of the finite element method on Octave. Octave is “a high-level language, primarily intended for numerical computations (...) that is mostly compatible with Matlab”. It may be used interactively or as a batch-oriented language.
Technically, OctMesh, constitutes an interface for the access from Octave to LibMesh, a C++ library for the numerical simulation of PDE by means of the finite element method (also with free license) developed, mostly, in the CFDLab of the University of Texas (although also it has counted with the contribution of other people and organizations). LibMesh facilitates the development of numerical simulations using 1D, 2D or 3D elements in parallel architectures (although it can work in sequential machines). It also includes methods for adaptive mesh refinement/coarsening.
OctMesh has been developed with the intention to unite the power of LibMesh with the ease of use of the Matlab language, and trying to facilitate the development from Octave of parallel numerical 1D, 2D or 3D, experiments.
Internally, it consists of a series of dynamic extensions for Octave (.oct-files), written in C++, that acts as a connection with LibMesh, introducing a space of additional functions that extend the Octave ones. These functions allow defining meshes, associating them finite elements spaces and quadrature formulae, mounting and solving the equation systems associated to the variational formulations of the EDP. All in a interactive way or in programs (.m-files) that use the Octave/Matlab interpreted language.
When creating these new functions in Octave, we have tried to conserve, as far as possible, the original syntax of the C++ classes that compose LibMesh. This has not been easy, because the Matlab language (and therefore Octave) is not Object Oriented. Nevertheless, some techniques was used that allowed to avoid this disadvantage successfully.
Although using an interpreted language implies certain performance loss in OctMesh, it exist a possibility that will be useful to advanced users: critic parts of the algorithm may be developed in C++ (with LibMesh) and used from Octave (with OctMesh).
Again, most of this is foggy to me. I will update if I use and/or understand more. In general, I just hope maybe someone will find it useful.
Labels:
libMesh,
Numerical software,
Octave,
OctMesh,
Programming
Subscribe to:
Posts (Atom)